Here is part one of the series Bits and Bytes with AIR. It includes the Introduction and basic explanations of terms you`ll find in the world of bits and bytes.
Download as PDF.
INTRODUCTION
When I started with programming back in 1999 (yes flash was my first “programming” experience) I basically saw two paths splitting in front of me. The one was the geeky programmers way were everything was told in 0`s and 1`s and the other was the cool graphic oriented arty multimedia web designers way were programming was just a necessary minor matter and were was a subtle chance to at least have some woman in your lecture courses.
I went well with this attitude throughout the years. I started with flash 5 and there was no real need to get into bits and bytes. From flash 5 to 6, 7 and 8 the pressure was still low. But then in 2006 Adobe released the flash player 9 and with it came new mysterious power in form of the ByteArray class. My first encounter with it was when I studied the Sound Object API and it`s soundSpectrum method. It took quite some brain tweaking until I got it to work but saying that I really understood it would be a lie. While I got worried by this I still did not felt the need to really get into this stuff. But I had the deep feeling that Adobe had a master plan to let us Flash developers down and let “real” C++ or better Assembler programmers take over our beloved flash platform. Then there was AIR and everything changed. I fell in love with AIR from the first minute and only had one problem with it. I had the feeling that the new tool Adobe was giving us was not feature complete. All the apps I wanted to build needed something that was not covered by the new API. After some hours thinking about getting frustrated I realized that the frightening ByteArray class could be part of the solution.
BINARY NUMBERS – IT`S STILL JUST NUMBERS
In our normal live we deal a lot with numbers. The number system we are most familiar with is the decimal number system. The decimal number system is a base 10 numeral system which basically means that we know ten symbols (0-9) called digits to represent numbers. When working with binary data we still deal with numbers but the symbols we have available are less. The binary system only knows two symbols 0`s and 1`s to represent any number. In the binary world those symbols are called Bits. If you`re are not familiar with the binary system you may ask how it`s possible to represent any possible number with just 0`s and 1`s. Counting in binary is very much similar to counting in decimal. In decimal you start counting with the 9 symbols you have like so:
001, 002, 003, 004, 005, 006, 007, 008, 009
When all symbols are used you add one digit to the left and reset the one before to zero. Now you restart incrementing those values.
010, 011, 012, 013, 014, 015, 016, 017, 018, 019, 020 and so on.
This is exactly the same in the binary world only that counting up is faster because we only have two symbols. So it goes like this:
0000, 0001, 0010, 0011, 0100, 0101, 0110, 0111 …
BITS AND BYTES
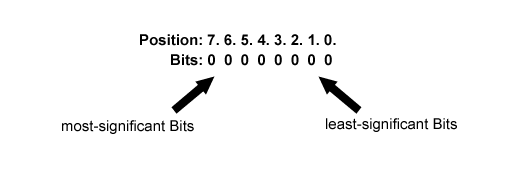
The symbols 0 and 1 that are used in the binary system are called bits in the computer world. A bit is the smallest information a computer can work with. Most of the time when you deal with binary data you will not deal with single bits but rather with collections of bits. Those collections are called a word. Those words can consist of different numbers of bits and the smallest collection used is a byte which consists of 8 bits. Because a Byte has 8 Bits it can describe integers between 0 and 255. There are two ways how to group Bits into a byte. The most common one is called Big-Endian were you start counting on the right site. So the Bits on the right site will carry lower values and the more Bits you go to the left the higher the values. That`s why the Bits on the right are called the least-significant Bits and the Bits on the left are called the most-significant Bits. As said earlier this way of ordering Bits into a Byte is called Big-Endian. The opposite of this is called Little-Endian were the least-significant Bits are on the left and the most-significant Bits are on the right.
In the last paragraph we said that a byte can represent integers with a value between 0-255. Often however we do not treat words as a representation of a number but rather as a container for Bits, were groups of Bits inside this container can carry their own information. Imagine for example you want to store the numbers 15 and 12. To do this you can use two Bytes like this.
00001111 = 15
00001100 = 12
We can see that in those two Bytes the most-significant Bits are not used. In this example 4 Bits for each Number are just wasted. To store our two numbers more efficiently we could rather store both numbers in one Byte like this:
1100 1111
The one who later analyses the Byte just needs to know that the first and the last 4 Bits each represent a Number.
When information is stored into a word like this we speak of a packed word. In order to analyze the content of a packed word we need to have tools to extract individual Bits from a word. When you check out the ByteArray class of the Flash Player you`ll see that the smallest information you can get is a Byte (ByteArray.readByte()). I order to analyze the individual Bits of a word bitwise operations will become a handy tool.
To Be Continued…